In injection molding, the molten plastic (fluid) flows through sprues and runners and gets filled inside the cavity.

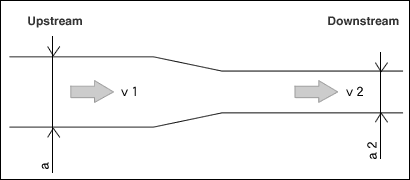
This phenomenon is expressed schematically as a fluid with viscosity flowing in a pipe.

When a viscous fluid flows through a pipe having a certain cross-sectional area, there is a basic equation of calculation called the "Flow Volume Equation" that expresses the basic state.

The volume Q of fluid flowing through the pipe per unit time can be obtained by multiplying the cross-sectional area of the flow path (pipe) and the flow speed of the fluid.

It can be understood from this equation that in order to increase the flow rate, either the cross-sectional area a of the flow path has to be increased or the flow speed of the fluid has to be increased.

In addition, when the flow rate is constant, the following equation becomes valid.

a1.v1 = a2.v2, where, 　　　a1：Cross-sectional area of the upstream flow path 　　　a2：Cross-sectional area of the downstream flow path 　　　v1：Upstream flow speed 　　　v2： Downstream flow speed

In other words, when the flow rate is constant, the fluid flows slowly when the cross-sectional area of the flow path is large, and the fluid flow speed becomes fast when the cross-sectional area of the flow path becomes small.

Therefore, when the molten plastic flows inside a thin runner or gate, the flow speed becomes high.

However, since the viscosity of the molten plastic changes with time, strictly speaking, the above equation will have to be corrected using a variety of factors.